- Решение неравенств
Поставьте вместо знака ? знак <, > или =.
- 28510 ? 11D16 (Ответ: 28510 = 28510 )
- 1111112 ? 11118 (Ответ: 6310 < 58510 )
- 6С16 ? 1010012 (Ответ: 10810 > 4110 )
- 5516 ? 1258 (Ответ: 8510 = 8510 )
- Числовые последовательности.
Расположите числа, записанные в различных системах счисления, в порядке возрастания:
- 3510, 368, 3А16, 1001012 (Ответ: 368, 3510, 1001012, 3А16 )
- 1110012, 648, 9Е16, 2510 (Ответ: 2510, 648, 1110012, 9Е16 )
- 728, 15610, 1010012, 8В16 (Ответ: 1010012, 728, 8В16, 15610 )
- 12D16, 768, 1000112, 54110 (Ответ: 768, 1000112, 12D16, 54110 )
- Рождение цветка.
Понаблюдаем за рождением цветка: сначала появился один листочек, затем второй … и вот распустился бутон. Постепенно подрастая, цветок показывает нам некоторое двоичное число. Если вы до конца проследите за ростом цветка, то узнаете, сколько дней ему понадобилось, чтобы вырасти.
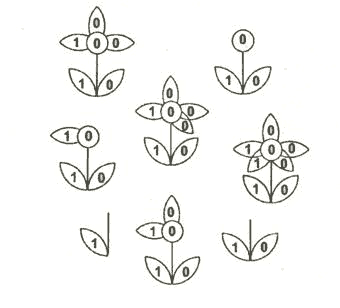
(Ответ: 100100012=145 дней)
- Числовой лабиринт.
Переведите числа, записанные в различных системах счисления, в десятичную систему счисления; затем полученные после вычисления числа замените буквами русского алфавита, которые имеют соответствующие порядковые номера; запишите полученное слово.
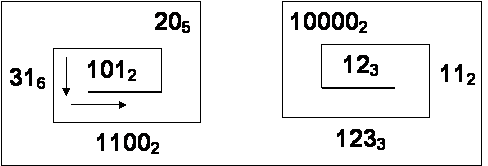
(Ответ: ДИСКОВОД)
5. Кроссворд
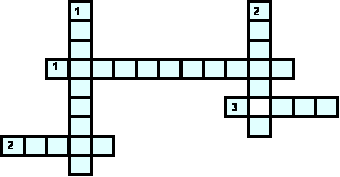
По горизонтали:
- Название системы счисления, в которой вклад каждой цифры в величину числа зависит от ее положения в последовательности цифр, изображающей число.
- Последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
- Символы, при помощи которых записывается число.
По вертикали:
- Знаменатель геометрической прогрессии, члены которой образуют базис позиционной системы счисления.
- Совокупность различных цифр, используемых а позиционной системе счисления для записи чисел.
(Ответы на кроссворд.
По горизонтали: 1. Позиционная. 2. Базис. 3. Цифры.
По вертикали: 1. Основание. 2. Алфавит.)
- В саду 100q фруктовых деревьев: из них 33q яблони, 22q груши, 16q слив и 17q вишен. Найдите основание системы счисления, в которой посчитаны деревья.
Ответ: 9
- В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Ответ: 6
- Земляне прилетели на далёкую планету Gamma Rays и разговорились с одним почтенным отцом семейства. Он рассказал, что у него много детей – 33 сына и 50 дочерей. Всего детей – 113, а годиков ему, соответственно, 101. А на самом-то деле сколько чего?

Ответ: 24 сына, 35 дочек, 59 детей, 50 лет отцу.
- У мальчика 35 шоколадных конфет и 113 карамельных, а всего конфет 152. Как это возможно? Сколько каких конфет в десятичной системе счисления?

Ответ: 23 шоколадные конфеты, 45 карамельных, 68 всего, 6-СС.
- Прилетел как-то к земной девушке красавице писанной ухажёр с планеты DOUBLE FINGERS и ну замуж её звать и похваляться, что де и зарабатывает он 1100000 долларов в месяц и апартаменты у него общей площадью 10100 квадратных метров, и одних машин у него 10 штук. Однако девица наша была с умом и учла, что всё это в двоичной системе. А сколько же по-нашему будет?

Ответ: 96$, 18 кв.м.
- А теперь представьте, что вы с ценным товаром – спичками – прилетели на планету Кин-дза-дза. У вас 10 000 упаковок по 20 рублей за упаковку. У них там шестнадцатеричная система счисления. Они, не разобравшись, всё раскупают по 20 своих кин-дза-дзовских рублей, которые вы потом спокойно меняете на свои десятичные. Какова же неожиданная прибыль?

Ответ: 120000 руб.
- За праздничным столом собрались 4 поколения одной семьи: дед, отец, сын и внук. Их возраст в различных системах счисления записывается так 88 лет, 66 лет, 44 года и 11 лет. Сколько им лет в десятичной системе счисления, если через год их возраст в тех системах счисления можно будет записать как 100.
Ответ: 80, 48, 24, 13.
- В бумагах одного чудака-математика найдена была его автобиография. Она началась следующими строками:
„Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте- всего 11 лет, -способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет, у меня была уже и маленькая семья из 10 детей. Жалованья я получал в месяц всего 200 рублей, из которых 1/10 приходилось отдавать сестре, так что мы с детьми жили на 130 руб. в месяц" и т. д. Чем объяснить странные противоречия в числах этого отрывка?
